To understand recursion, one must first understand recursion.
~ Stephen Hawking

• I think recursion is one of the most useful tools of programming and it really gives the essence of optimized and efficient programming to me.

Why must u bother about this article?

• I know there are many great and informative articles about recursion but tbh most of us don't make it to the finish.
• This is a fresh perspective of a student (myself) who learned this powerful programming tool quite recently

• But I'm pretty sure I won't because of its functionality and power 😎 This article will try to make recursion as easy as possible

Definations

• Wikipedian definition:

Recursion is the process of repeating items in a self-similar way

That was really helpful, Right?

To really understand recursion think of a long line in which you are standing in a certain position and you don't know what position it is so what you do is ask a person in front of you but because it's a long the line that person also don't know his position so he/she does the same thing (asking the person in front of him), this goes on until it the person standing first in line is asked here he know his position that is first so this person tells this position to the second then the second tells the third and this goes on and you get your answer (your position in the line)

So let's understand what this long-line story concludes

Algorithmically

• Here what you're doing is using a divide and conquer or decrease and conquer technique by making your complex problem ( of finding you're position in the line ) into smaller ones (asking every next person).
• And the first person in line is actually the base case that is where the recursion stops and returns the answer to the question asked by the 2nd person who returns the answer for the 3rd one and it goes on until the answer Is obtained.

Semantically

• What you're doing is calling a function inside itself
• With a base case to stop recursion because we don't want an infinite recursion.

EXAMPLES

1. Multiplication

• Imagine multiplying a into b but you only have the addition operator available so what we do is add a to itself b times.

• So the simple iterative solution would be as follows :

  def mut_iter( a , b )
    i = 0
    while b > 0 :
       b -= 1
       i += a    
    return i
  

• But now think about this recursively i.e. a + a + ........ + a }---> that is a b times but also a +a + .........+ a }---> that is a + [a ( b-1 ) times]

Recursive Step:

• It's reducing a problem to a simpler version of itself

• here a + a*( b-1 ) is a recursive step

Base case :

• Its the simplest case which can be solved directly
• here b = 1 is the simplest case that can be solved directly by returning the answer as a

The recursive solution can be written as follows:

def mult ( a, b ):
    if b == 1 :
        return a
    else:
        return a + mult ( a, b-1 )

2. Factorial

• Finding factorial is one of the most common examples of recursion.
• So basically what we know about factorial to use it as a base case would be: n = 1 ---> n! = 1
• Therefore the recursive solution will look as follows:

  def fact(n):
     if n == 1:
        return 1
    else:
        n * fact ( n-1 )
  

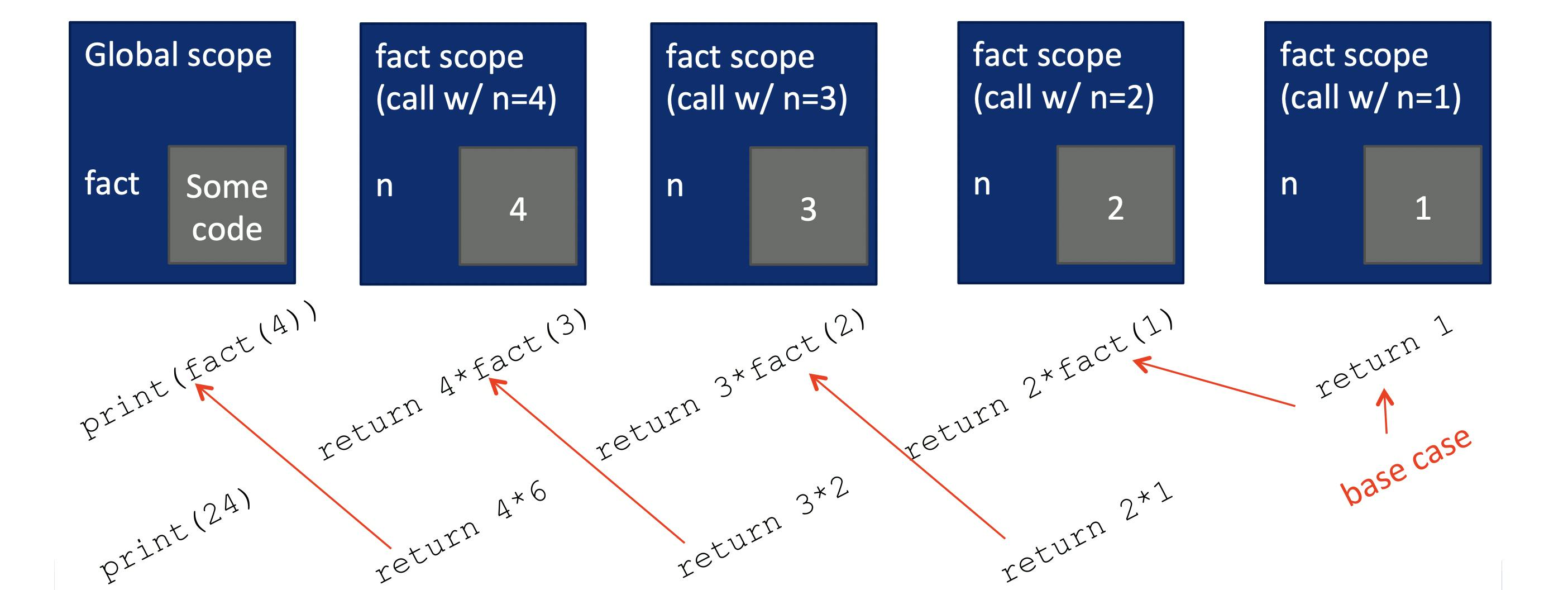
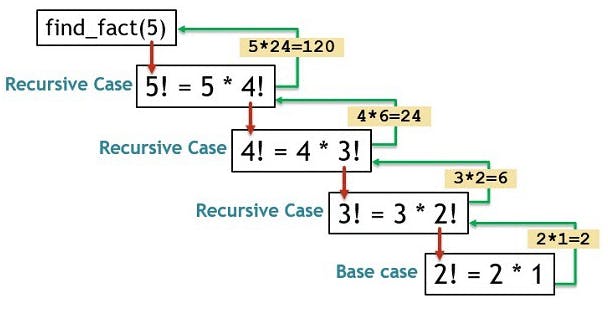
• As we are calling the function inside itself it creates a local scope for each of the recursive step and returns the value when reached the base case.
• The efficiency of recursion due to the creation of a temporary local scope depends, it might be efficient in some languages and might not in others.

📌 Note:- If you aren't familiar with the concept of scoping you can refer to some articles below:

saltycrane.com/blog/2008/01/python-variable..

realpython.com/python-scope-legb-rule/#unde..

• Let's look at the iterative solution for the same:

  def fact_itr (n):
   prod = 1
   for i in range(1,n+1):
      prod *= i
   return prod
  

  OR

  def fact_itr ( n ):
   b = n - 1
   while b > 1:
          n = n*b
          b = b - 1
   return n
  

• Recursions may be efficient from the programmer's POV and sometimes may be inefficient from the computer's POV

Some Good Examples you can check out :

1. Towers of Hanoi

1. Fibonacci Numbers (great example with multiple base cases)

1. Finding Palindromes

1. Finding Greatest Common Divisor (GCD)

📌 All of these examples can also be written iteratively which can be a fun assignment and some of these examples will also make you realize the power of Recursion😎, so try to do them on your own.