Merge-Sort

An Oldie but a Goodie

• Merge sort is an old algorithm while keeping modern computation in mind.

• Founded in 1945 by John von Neumann

• It's more efficient than some of the algorithms used to solve the same problem it does such as insertion sort or bubble sort in the worst-case scenario.

• The merge-sort algorithm falls under the divide-and-conquer paradigm.

The Sorting Problem

• It's a problem that the merge-sort algorithm solves.

  

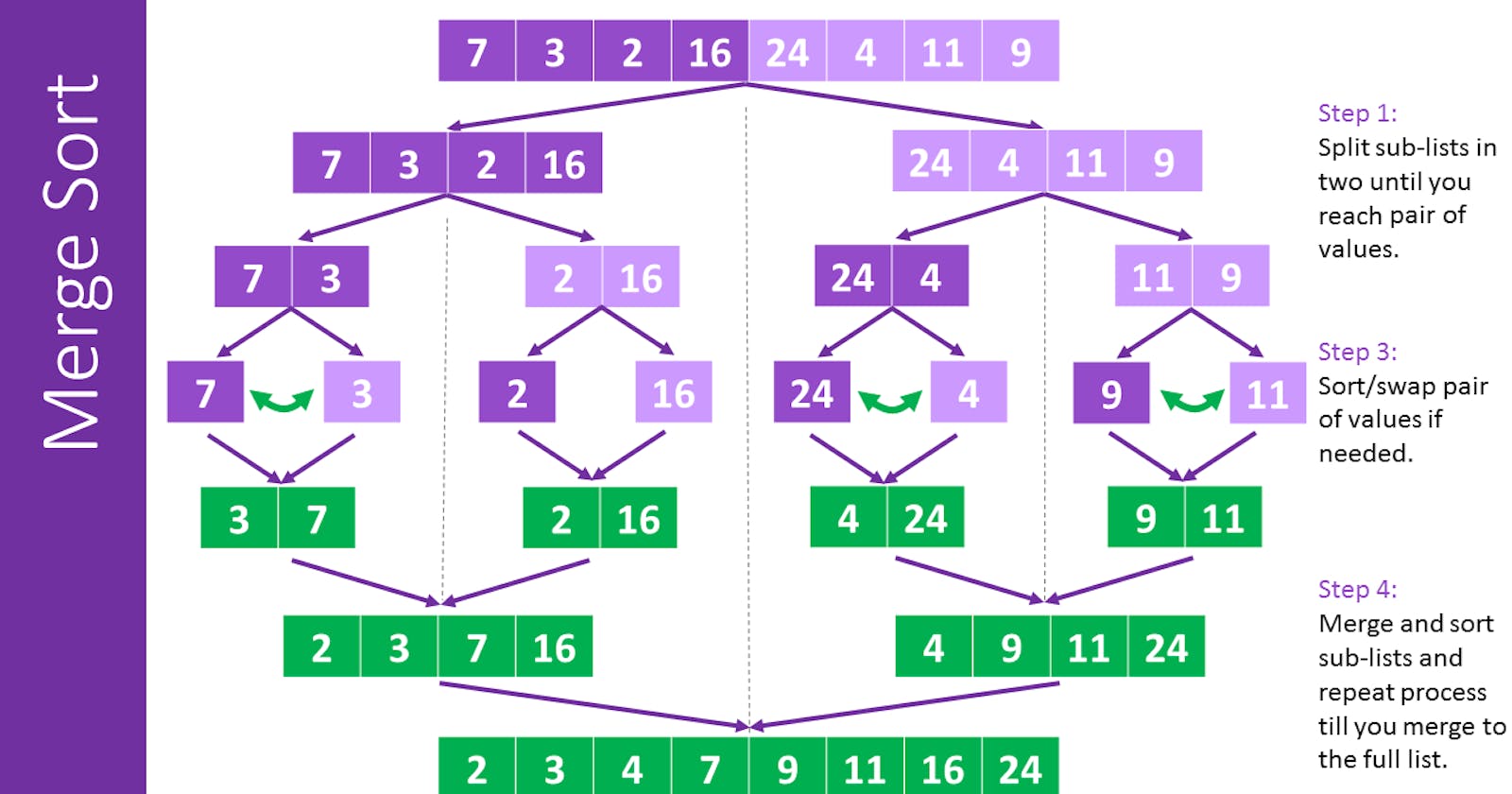
• Here we have an array of numbers all distinct and even (To get an upshot of the merge sort algorithm)

• We often solve this problem recursively i.e, converting it into small subproblems, here into smaller arrays

• After recursive calls and sorting each sub-array we merge the output arrays (we'll see the detailed pseudocode following)

Merge Sort : Pseudocode

C = Size of input array (n) ---> k variable to iterate through
A = First sorted array ---> i variable to iterate through
B = Second sorted array  ---> j variable to iterate through

for k = 1 to n:
  if A(i) < B(j):
    C(k) = A(i)
    i++
  if B(j) < A(i):
    C(k) = B(j)
    j++

(This Pseudocode addresses the merge-sort problem after getting A and B output from recursive steps)

Merge-Sort Running Time

For those who don't know what a running time is, it's just like No. of lines executed

• If we count no. of operations in the above example we get tentatively 4n + 2 operation [initializing A and B variable (2), and for each iteration, we perform 4 operations (4n)]

• We can liberally consider 4n + 2 as 6n because we generally ignore constant terms/low-order terms considering the running time (as we are oriented towards worst-case analysis)

• There is a Claim that Merge sort requires =< 6n(log₂(n)) + 6n operations to sort n numbers

PROOF

(Using recursion tree)

To prove the claim let's understand how the logarithmic function works to get a general idea, consider log₂(n) ( log to the base 2 ) what does it mean, it means that how many times you have to divide n by to get output as less than one or so, eg:

let n = 32 => log₂(32) = 5

because if you divide 32 by 5 times it gives you output less than one

Similarly, if we try to find the number of levels in the above recursion tree we get to know the root node is split into subnodes until we get to the level where it's the base case i.e, <= 1, which implies that the log₂(n) spits out the number of levels in the tree.

hence j = 0, 1, 2, 3,.., log₂(n) , considering j as number of levels and n = no. to be sort

Now according to the recursion tree, we can observe at each level there is work done and each level has 2^j problems and the size of each problem is n/2^j.

But we already computed work required for each problem to merge is 6n hence the total runtime for each level is: 2^j * 6(n/2^j )

This cancels out 2^j which gives independent 6n as the runtime for each level

and for the entire merge sort, we have 6(log₂(n) + 1 ) i.e, 6n(log₂(n)) + 6n

here log₂(n) is the number of levels and 1 is the root node.

Hence, Proved 😁🎉

Note: Here Merge-sort analysis is explained assuming the reader already knows the recursion algorithm, To learn more about Recursion briefly you can refer to my article :

Learn Recursion in 5 minutes